- ✓ Start direct
- ✓ Kostenloos
- ✓ Tijdsduur 60 minuten
- ✓ Inclusief oefenen
- ✓ Vo / mbo niveau
1: INLEIDING
Voor rekenen is in Nederland het tientallige talstelsel de standaard.
Het tientallige stelsel wordt zo genoemd omdat het bestaat uit tien cijfers. Namelijk de cijfers 0 tot en met 9.
Een andere benaming voor dit stelsel is het decimale getallenstelsel.
Het grondtal is tien. Waarom dat zo is lees je verderop. Het is een leuk feitje.
Een computer rekent heel anders. Een computer gebruikt het binaire talstelsel.
Het binaire stelsel bestaat slechts uit twee cijfers. Namelijk 0 en 1. Het grondtal in het tweetallige stelsel is
twee.
Hoe je kunt rekenen met bits en met bytes wordt hieronder uitgelegd. Ook vind je op deze pagina weer
een handige rekentool en een link naar een interactieve oefening. Oefenen kan tegenwoordig ook in de dark mode.
Vind je het prettig om te werken met een donker scherm klik die optie dan eenvoudig aan. Onderaan deze pagina
staat een YouTube-filmpje met uitleg over de rekentool.
1.1 Wat leer je?
Na het bestuderen van dit onderdeel kun je procenten uitrekenen:
- ● Je weet wat het decimale en wat het binaire talstelsel inhoudt.
- ● Je kunt het verschil tussen een bit en een byte uitleggen.
- ● Je kunt rekenen met bits en bytes.
- ● Je weet hoe je eenvoudig een omrekentabel kunt maken.
- ● Je weet wie Blaise Pascal is.
- ● Je weet hoe de rekentool werkt.
2: UITLEG
Rekenen met nul en één
Rekenen met nullen en enen zoals een computer dat doet komt misschien een beetje vreemd over. Maar zodra je door hebt hoe het werkt is het echt niet moeilijk meer. Zolang je maar onthoudt dat het gehele stelsel slechts uit twee cijfers bestaat, namelijk de cijfers 0 en 1. Dat lijkt overzichtelijk maar omdat het vaak een lange rij van nullen en enen is wordt het complex.
> Dit is een voorbeeld van een byte: 11010110.
Een byte heeft 8 posities die bits worden genoemd. Een byte estaat dus uit acht nullen en enen. Waar we in het decimale talstelsel 0, 1, 2, 3, 4, 5, 6, 7, 8 en 9 gebruiken, gebruikt het tweetallig stelsel dus uitsluitend een 0 en een 1. De byte ken je inmiddels. Dat zijn acht nullen en enen achter elkaar. Zoals je in het voorbeeld hierboven kan zien.
Rekenen met bits
We gaan onderscheid maken tussen het tientallige talstelsel en het tweetallig talstelsel. Dat ook wel het binaire stelsel wordt genoemd. Waarom we dit doen is eenvoudig te beantwoorden. We kunnen weinig met alleen nullen en enen beginnen. We hebben iets anders nodig om de code te kunnen begrijpen. En dat is het tientallige talstelsel in dit geval. Als we de bits en bytes omrekenen naar getallen die we kennen wordt het pas zinvol.
Het tientallige talstelsel
Het tientallige stelsel bestaat uit de cijfers 0, 1, 2, 3, 4, 5, 6, 7, 8, en 9. Het grondtal bij dit stelsel is 10. Omdat we deze getallen met tien vingers kunnen uitrekenen. De priemfactoren zijn 5 en 2. Tien is alleen door deze twee cijfers te delen zonder dat er een rest overblijft. Het eerste getal na de negen is 10. En alle veelvouden daarvan eindigen ook op een nul. Namelijk 100, 1.000, 10.000 enzovoort. Een ander bekend stelsel is bijvoorbeeld het stelsel met Romeinse cijfers (in ontwikkeling). Daarbij wordt bijvoorbeeld het getal 1.251 weergegeven als MCCLI. Maar dit zouden we ook in binaire code kunnen opschrijven. Het getal 1.251 dat dus uitgedrukt in Romeinse cijfers MCCLI is, wordt met behulp van het binaire talstelsel 10011100011.
Het tweetallige talstelsel
Zoals gezegd bestaat het binaire talstelsel dus uit 0 en 1. Computers gebruiken deze bits om berekeningen te kunnen maken. Waarbij een 0 uit betekent en de 1 aan betekent. Dit gebeurt letterlijk zo met het aan en uit gaan van een transitor in de hardware van de computer. Om snellere en krachtigere berekeningen te kunnen maken werd er van bits overgestapt op bytes. Zoals je inmiddels weet bestaat een byte uit acht bits. Om diezelfde reden werden later ook 16-bits, 32-bits en 64-bits uitgevonden. We noemen deze overigens nog steeds bytes. In dit geval respectievelijk 2 bytes (16), 4 bytes (32) en 8 bytes (64).
Vergelijken van de twee stelsels
Vervolgens kunnen we beide talstelsels boven elkaar leggen. Er ontstaat dan dit:
TABEL: 1
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | decimale talstelsel |
| 0 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | 1001 | binaire talstelsel |
Eenvoudig tot tien tellen zoals wij dat op onze vingers kunnen doen ziet er in het biniare stelsel dus als volgt
uit:
1, 10 , 11, 100, 101, 110, 111, 1000 en 1001.
Waarbij dus bijvoorbeeld het cijfer 4 gelijk staat aan 100 in een binaire getal. Nu we precies weten hoe de getallen zich tot elkaar verhouden kunnen we er ook meegaan rekenen.
Omrekenen van getallen
Maar hoe komen we nu aan bijvoorbeeld het binaire getal 100 dat gelijk staat aan het getal vier? Daarvoor moet je onderstaande tabel begrijpen.
TABEL: 2
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | een byte |
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | omrekenen |
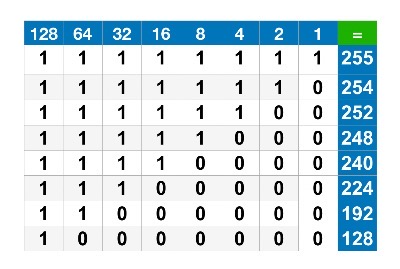
Als het binaire getal, in dit geval een byte, allemaal enen bevat is het omgerekende getal 255. Je kunt dit eenvoudig uitrekenen door 128, 64, 32, 16, 8, 4, 2 en 1 bij elkaar op te tellen. Samen is dat 255. Om dus 4 om te rekenen naar het binaire getal 100 gebeurt er het volgende.
TABEL 3
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | drie bits |
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | omrekenen |
Je ziet dat er slechts een 1 staat. En deze 1 staat boven het getal 4. Met de twee nullen erachter van 2 en 1 vormt dit dus de waarde 4. Alle nullen voor de 1 mag je weglaten. Net zoals dat gebeurt bij het rekenen met decimale getallen die je bijvoorbeeld optelt, aftrekt, vermenigvuldigt of deelt. Het getal 4 is dus in het binaire talstelsel 100. Op deze wijze kun je dus elke bit of byte omrekenen naar een heel getal of omgekeerd. Maak eenvoudig een tabel met twee rijen en vul alvast de waarden van de bits in. Daarna zet je een 1 boven elke waarde die je nodig hebt om een getal om te rekenen. Vind je het nog steeds lastig? Gebruik dan de handige rekentool. Waar de cijfers 128, 64, 32, 16, 8, 4, 2 en 1 vandaan komen wordt later in de stof behandeld.
3: VOORBEELDEN
Voorbeeld 1: hoeveel is 11010 binair omgerekend naar het decimale talstelsel?
TABEL 5
| 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | vijf bits |
| 0 | 0 | 0 | 16 | 8 | 0 | 2 | 0 | is 26 |
Voorbeeld 2: hoeveel is 11010110 binair omgerekend naar het decimale talstelsel?
TABEL 6
| 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | een byte |
| 128 | 64 | 0 | 16 | 0 | 4 | 2 | 0 | is 214 |
Voorbeeld 3: hoeveel is 00000001 binair omgerekend naar het decimale talstelsel?
TABEL 7
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | een bit |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | is 1 |
4: NASLAGWERKEN
Begrippenlijst van A - Z
In de financiële begrippenlijst vind je alle woorden die in de tekst blauw zijn gekleurd. Met uitzondering van weblinks. Weblinks zijn te herkennen aan een streep onder het woord, en ze zijn klikbaar.
Wet- en regelgeving
In wet- en regelgeving vind je alle wetsartikelen en regelgeving. Je kunt deze woorden herkennen in de tekst aan hun paarse kleur.
Lijst met afkortingen
In de lijst met afkortingen vind je alle woorden die in de tekst oranje zijn gekleurd.
Je vindt deze naslagwerken in de menubalk. Ze openen in een apart tabblad dus kun je ze naast de theorie gebruiken.
5: TEST JE KENNIS
Je kunt nu een interactieve oefening maken waarbij automatisch jouw eindscore wordt uitgerekend. Klik daarvoor op oefenen onderaan deze pagina. Wil je liever oefenen met rekenen in Microsoft Office Excel klik dan op 'spreadsheet openen' (in ontwikkeling).
6: IN DE PRAKTIJK
In de praktijk heb je deze kennis altijd nodig wanneer je een loopbaan ambieërt in de IT. Of als je als zelfstandig IT-ondernemer wilt gaan werken. Uiteraard werk je dan niet dagelijks met nullen en enen maar je moet het principe wel begrijpen. Werken in de IT-sector vereist voldoende kennis van wiskunde. Het is namelijk ook de basis van het begrijpen van veel programmeertalen waarbij 1 en 0 staan voor true en false. Op dat moment heet het geen 1 of 0 maar een boolean.
Wist je dat de eerste rekenmachine werd uitgevonden in het jaar 1645 door de Franse wis- en natuurkundige Blaise Pascal. Zijn vader die voor de belastingen werkte kon meteen gebruikmaken van deze handige uitvinding. Kijk maar eens op de Wikipedia pagina Blaise Pascal.
Meer rekenen
Dit was een specifiek onderwerp waarbij je hebt leren rekenen binnen het binaire stelsel. Met nullen en enen dus. Je kunt nog meer berekeningen oefenen. Een greep uit eenvoudige wiskundige berekeningen vind je hieronder. Je vindt er naast uitleg over het rekenonderwerp ook weer een handige rekentool. Bekijk het filmpje op YouTube met uitleg over hoe je de rekentool het beste kunt gebruiken. Ook vind je bij elk onderwerp een interactieve oefening zodat je de theorie goed 'onder de knie' kunt krijgen. De eindscore wordt na elke oefening automatisch uitgerekend en getoond.
Vul de gevraagde gegevens in en klik op berekenen.
Wil je precies weten hoe je het onderstaande formulier correct invult? Kijk dan eerst dit YouTube-filmpje.
INSTRUCTIEVIDEO (1.30 minuten)
Omrekenen van getallen uit het binaire talstelsel doe je eenvoudig met deze handige rekentool. Leer getallen
van binair omzetten naar getallen uit ons decimale talstelsel of andersom. Kies uit de twee opties die
de rekentool heeft. Klik op berekenen en de uitkomst wordt direct getoond. Een byte heeft acht bits en de
waarde in het decimale talstelsel is maximaal 255.
Na 1 minuut en dertig seconden weet je precies hoe het werkt.
 BEDRIJFSREKENEN.NL
BEDRIJFSREKENEN.NL