- ✓ Start direct
- ✓ Kostenloos
- ✓ Tijdsduur 60 minuten
- ✓ Voor po / vo / mbo
Breuken ontstaan wanneer je een getal door een ander getal deelt. Maar let op: dit wil niet zeggen dat er altijd een breuk ontstaat. Wanneer je het getal 10 deelt door 5 ontstaat er wel een nieuw getal, namelijk 2, maar dit is geen breuk. Dit is een geheel getal.
Hoe herken je een breuk?
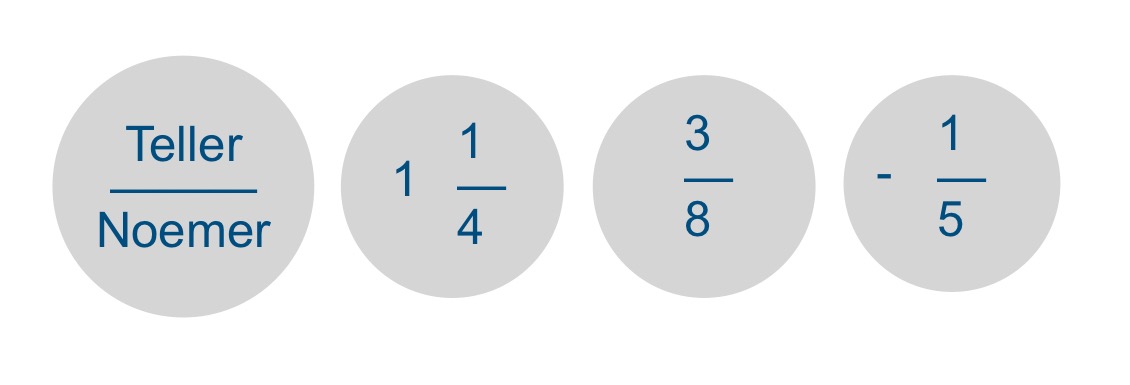
Een breuk kun je herkennen aan twee getallen met een streep er tussen. Dit leesteken wordt ook wel de breukstreep genoemd. Kenmerkend aan een breuk is dat het een teller en een noemer heeft. De teller staat voor de breukstreep / en de noemer erachter. Soms zie je een breukstreep staan in de vorm van een diagonale streep (/) en soms als een liggende streep (-). Hierboven in de afbeelding zijn dus ook alle drie breuken. Om te kunnen rekenen met breuken moet eerst de hele ervoor verwijderd worden. In het voorbeeld hierboven is dat de 1 in de breuk 11⁄4. Hierover later meer. De breuk met het minteken ervoor is een negatieve breuk. Deze kan ontstaan als je twee breuken van elkaar aftrekt waarbij de teller van de tweede breuk groter is dan van de eerste breuk. Bijvoorbeeld 1/3 - 2/3 = -1/3. Een breuk kan ook precies op nul uitkomen. Dit gebeurt bijvoorbeeld als je 1/3 van 1/3 aftrekt. De uitkomst is dan 0.
Hoe reken je met breuken?
Je kunt met breuken rekenen. Breuken kun je bij elkaar optellen (+) maar ook van elkaar aftrekken (-). Hetzelfde geldt voor delen (:) en vermenigvuldigen (x). Alle vier de manieren om met breuken te rekenen worden hieronder uitgelegd. Je kunt met breuken zelfs machtsverheffen. Maar dat wordt hier niet behandeld. De rekentool onderaan de pagina kun je gebruiken om breuken bij elkaar op te tellen, van elkaar af te trekken, te vermenigvuldigen met elkaar, of ze te delen. Vul twee breuken in waarvan de noemers hetzelfde zijn en waar geen hele voor staan. Klik dan op berekenen. Het juiste antwoord wordt direct getoond. Maar eerst een korte uitleg over een geheel getal, vereenvoudigen, gelijknamig maken van breuken met behulp van delen door de grootste gemene deler (ggd) of vermenigvuldigen met het kleinste gemene veelvoud (kgv).
Een geheel getal
Een geheel getal kun je ook als een gewone breuk uitschrijven. Dat gaat als volgt: Deze onechte breuk 5⁄1 is gelijk aan het gehele getal 5. Omdat hier eigenlijk het volgende staat: De breuk 5⁄1 staat gelijk aan 1 x 5 = 5, oftewel 5 keer de breuk 1⁄1. Je vermenigvuldigt simpelweg de noemer met de teller. Alle breuken met een 1 als noemer zijn feitelijke gehele getallen met een waarde die de teller aangeeft. Dus 3⁄1 is 3, en 16⁄1 is 16 en 312⁄1 is 312. Zo simpel is het. Het is belangrijk om dit te onthouden. Want soms moet je rekenen met een breuk en een geheel getal. Nu weet je dus hoe je in zo'n geval eerst dat gehele getal in de vorm van een breuk kunt opschrijven. Daarna is het zoals rekenen met elke andere twee breuken, zoals hier bijvoorbeeld 3⁄1 x 1⁄4.
LET OP: breuken die er zo uitzien 1⁄1 zijn in feite gehele getallen. In dit geval het getal 1.
Vereenvoudigen
Bij breuken ga je op zoek naar de meest eenvoudigde vorm. De grootste gemene deler (ggd) helpt je daarbij. Een breuk vereenvoudig je door de teller en de noemer door hetzelfde getal te delen zonder dat er een rest overblijft. Een breuk met een teller 3 en de noemer 9, oftewel 3⁄9, kun je allebei delen door 3. De breuk 1⁄3 ontstaat dan. En die kun je niet meer delen. Een 1 delen levert namelijk een gebroken getalswaarde op en dat wil je niet.
De grootste gemene deler vinden
Je gaat hierbij op zoek naar het grootste getal waar de teller en de noemer beiden door te delen zijn en dat niet het getal 0 is. Ze noemen dit
ook om die reden de grootste gemene deler (ggd). Maar er mag zowel voor de teller als voor de noemer geen nieuwe breuk ontstaan.
Er onstaat dus geen 'rest' wordt er dan gezegd.
Bijvoorbeeld 4⁄8 is te delen door 4. De nieuwe vereenvoudigde
breuk is dan 1⁄2. Deze breuk kun je niet kleiner maken zonder
dat er opnieuw een breuk ontstaat. De
breuk 5⁄8 kun je niet verder vereenvoudigen. Als je de
teller deelt door bijvoorbeeld 2 ontstaat er een nieuwe breuk in de
teller. Dit is dan 2,5. En dat wil je niet. Je zou de teller wel door 5 kunnen delen, maar helaas de noemer niet.
Het kleinste gemene veelvoud
Je hebt hierboven zojuist geleerd hoe je met behulp van de grootste gemene deler (ggd) een breuk gelijknamig kunt maken. Maar soms zijn twee breuken niet op die manier gelijknamig te maken. Wanneer je bijvoorbeeld de breuken 2⁄5 en 1⁄4 bij elkaar wilt optellen. Je kunt 5 delen door 5 en 1 zonder dat er een rest ontstaat. Je kunt 4 delen door 4, 2 en 1 zonder dat er een rest ontstaat. Maar een gemeenschappelijke deler is er niet. In zo'n geval gebruik je het kleinste gemene veelvoud (kvg). Je gaat nu vermenigvuldigen in plaats van delen.
De noemer 5 uit de eerste breuk (2⁄5) kun je met 4 vermenigvuldigen. Je kunt de noemer 4 uit de tweede breuk (1⁄4) vermenigvuldigen met 5. Beide noemers zijn dan gelijk aan elkaar, namelijk 20. Let op dat je ook de tellers vermenigvuldigt met dezelfde getallen 5 en 4. Anders klopt de berekening uiteindelijk niet. Nu de breuken 8⁄20 en 5⁄20 gelijknamig gemaakt zijn kun je ze eenvoudig bij elkaar optellen. De uitkomst 13⁄20 is niet verder te vereenvoudigen.
LET OP: kun je breuken niet gelijknamig maken met behulp van de ggd, kies dan voor het kvg.
Volg altijd deze twee stappen als je gaat rekenen met breuken:
Stap 1: vereenvoudig de breuk
De breuk 21⁄4 kun je ook opschrijven als 9⁄4. Het getal 2 voor de breuk is een geheel getal dat gelijk is aan 2 x de noemer. Oftewel 2 x 4 = 8. Vervolgens tel je daar de waarde van de teller bij op. In dit geval dus 1. Dit mag je zo uitrekenen voor elke breuk die met een geheel getal begint. Dit noem je de hele binnen de breuk brengen. Vervolgens ga je op zoek naar de meest eenvoudige vorm. In dit geval is dat nog steeds 9⁄4. Omdat 9 en 4 niet meer te delen zijn zonder een gebroken getal over te houden. Een voorbeeld uitwerking zie je hieronder staan:
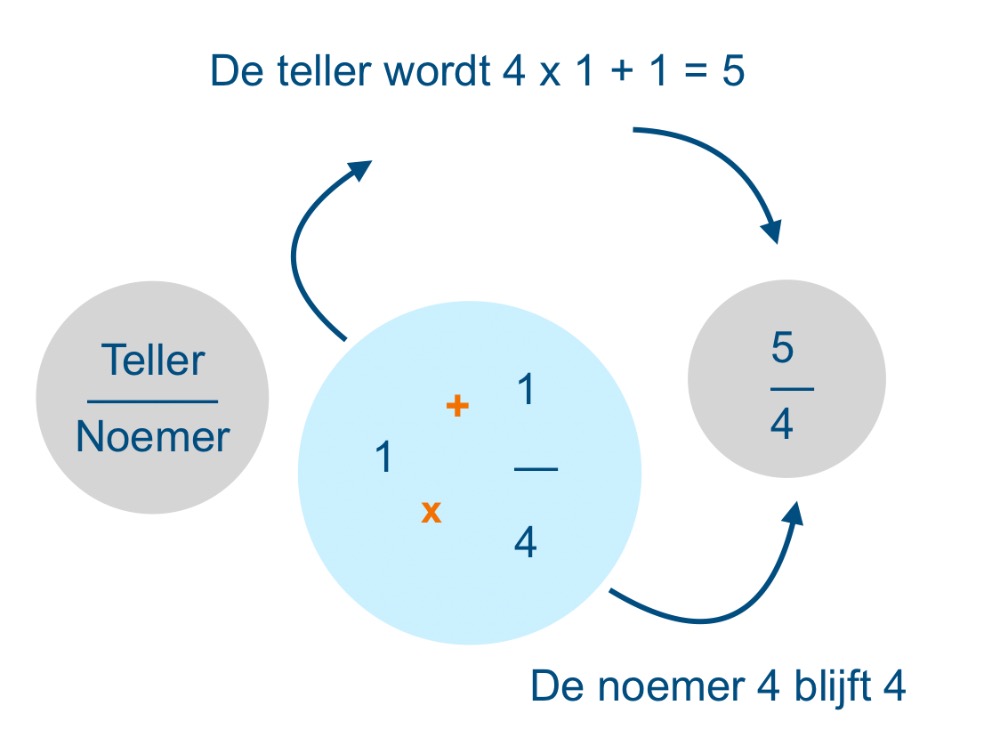
Stap 2: vervolgens ga je de breuken gelijknamig maken
Twee breuken gelijknamig maken betekent dat de noemers dezelfde getalswaarde moeten krijgen. Dit doe je voordat je gaat optellen (+) of aftrekken (-). Ga je breuken met elkaar vermenigvuldigen of delen dan hoef je de noemers niet eerst gelijk te maken.
Dus bij de twee breuken 3⁄4 en 6⁄8,
deel je 6⁄8 door 2. Er blijven nu twee breuken over met
een 4 als noemer.
Namelijk,
3⁄4 en 3⁄4.
Nu kun je met de breuken elke berekening maken
die je wil. Valt het je op dat de eerste breuk 3⁄4 al
vereenvoudigd is? Je kunt namelijk
3⁄4 niet kleiner maken. Terwijl dit wel kan bij de
andere breuk, 6⁄8.
LET OP: je hoeft breuken niet te vereenvoudigen bij vermenigvuldigen of delen. Wel moet de hele ervoor weg.
Breuken bij elkaar optellen (+)
Breuken bij elkaar optellen kan alleen wanneer beide breuken dezelfde noemer hebben. Je hebt deze breuken dus al vereenvoudigd en gelijknamig gemaakt. Je telt bij het optellen alleen de tellers bij elkaar op. De noemer blijft hetzelfde.
Bijvoorbeeld: 1⁄5 + 3⁄5 = 4⁄5
Breuken van elkaar aftrekken (-)
Het van elkaar aftrekken van breuken is nu niet moeilijk meer. Het gaat namelijk op dezelfde wijze als breuken bij elkaar optellen. Wederom moeten de noemers wel gelijk zijn. Zijn de noemers niet gelijk dan moet je beide breuken dus eerst nog gelijknamig maken. Staat er nog een hele voor een van de breuken, dan moet je die binnen de breuk brengen. Dit heb je hierboven zojuist kunnen lezen. Breuken van elkaar aftrekken doe je net zo als bij optellen alleen maar met de tellers. De noemer blijft hetzelfde. In het geval van breuken van elkaar aftrekken kan dus ook de al eerder genoemde negatieve breuk ontstaan. Verderop in de tekst leer je daar meer over.
Bijvoorbeeld: 4⁄5 - 2⁄5 = 2⁄5
Breuken met elkaar vermenigvuldigen (x)
Breuken met elkaar vermenigvuldigen lijkt misschien ingewikkeld maar dat is het niet. Breuken met elkaar vermenigvuldigen gaat als volgt: vermenigvuldig de teller met de teller (teller x teller) en vermenigvuldig vervolgens de noemer met de noemer (noemer x noemer). De noemer blijft nu niet meer gelijk zoals dat bij optellen of aftrekken wel zo is.
Bijvoorbeeld: 1⁄5 x 2⁄3 = 2⁄15
LET OP: soms kun je de uitkomst nog vereenvoudigen. In dit geval niet.
Breuken door elkaar delen
Als laatste kun je breuken ook nog door elkaar delen. Dit is wel lastiger dan optellen (+), aftrekken (-) of vermenigvuldigen (x). Maar er is een trucje. En die gaat als volgt: Stel je wilt 3⁄4 en 5⁄8 door elkaar delen. Dan is dat hetzelfde als 'vermenigvuldigen met het omgekeerde'. Je draait in dat geval de laatste van de twee breuken gewoon om en daarna vermenigvuldig je ze met elkaar. Zoals je hier ziet. 3⁄4 x 8⁄5 = 11⁄5
LET OP: Delen van breuken is vermenigvuldigen met het omgekeerde.
Negatieve breuken
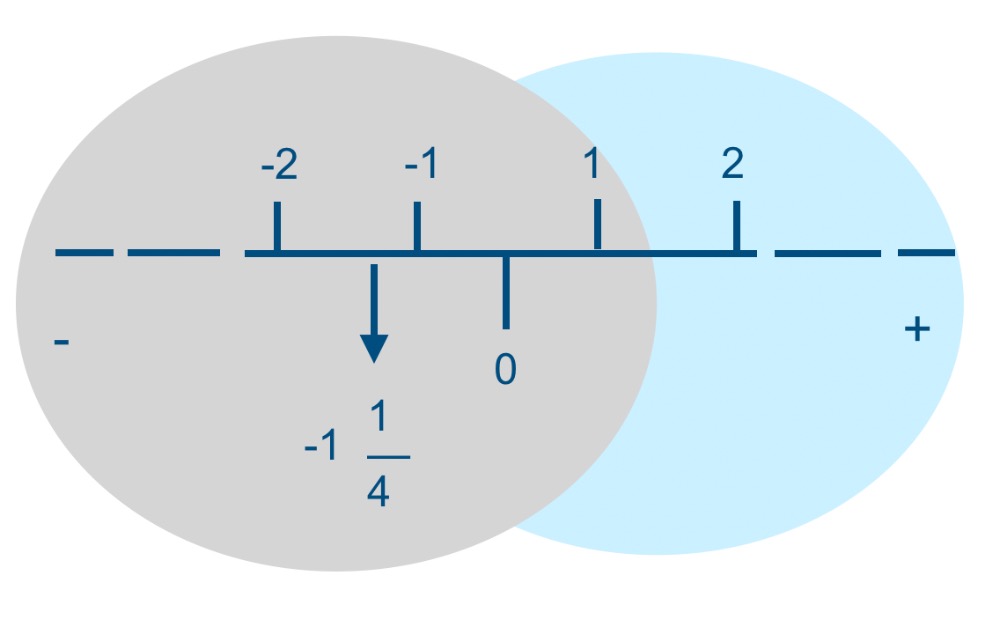
Bovenaan de pagina zag je in de afbeelding al even een negatieve breuk staan. Een breuk met een minteken (-) ervoor. Zo'n breuk kan ontstaan wanneer je gaat rekenen met breuken. Het voorbeeld dat al gegeven werd van 1/3 - 2/3 = -1/3, levert zo'n negatieve breuk op. Het is standaard om het minteken in zo'n geval voor de breuk te zetten. En dus niet voor de teller of de noemer waar het minteken eigenlijk ontstaat. Je ziet hier een afbeelding van een x-as met een nulpunt en de negatieve waarden -1 en -2. En ook de positieve waarden 1 en 2 staan op diezelfde x-as. De breuk -11⁄4 bevindt zich tussen - 1 en -2.
Aanvullende informatie
Euclides van Alexandrië wordt beschouwd als de grondlegger van de moderne wiskunde. In zijn meest bekende werk genaamd elementen leidt hij bepaalde eigenschappen af van gehele getallen. Zijn algoritme kun je gebruiken om de grootste gemene deler te vinden. Het is ook naar hem vernoemd. Wil je hier meer over te weten komen? Kijk dan eens op deze Wikipedia pagina: Euclides van Alexandrië.
Wil je oefenen met deze lesstof klik dan hier oefenen rekenen met breuken.
Vul de gevraagde gegevens in en klik op berekenen.
Wil je precies weten hoe je het onderstaande formulier correct invult? Kijk dan eerst dit filmpje met ondertiteling. Het is helaas nog niet gelukt om er audio aan toe te voegen.